Markoff numbers

A Markoff number (named after Andrei A. Markoff) is a number that appears in a positive integer solution to the equation a² + b² + c² = 3abc (known as the Markoff equation).

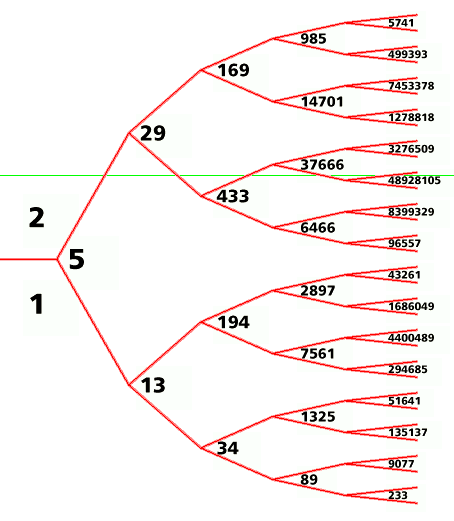
(1,1,1) and (1,1,2) satisfy the Markoff equation; all other solutions can be cataloged in a tree as shown below. The red lines partition the plane into open-ended regions, and each region is labeled with a number. The numbers in the three regions around any vertex constitute a triple (a,b,c) that satisfies the Markoff equation. For example, the solutions (1,2,5), (2,169,985), and (34,1325,135137) are associated with vertices in the tree below.

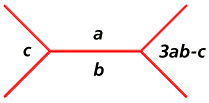
Simple algebra will show that if the triple (a,b,c) satisfies the Markoff equation, so does (a,b,3ab-c). This relationship is the basis for the construction of the tree; the four Markoff numbers in the regions around any two connected vertices are related to one another as shown below. The angles of the red lines vary, and aren't important; what counts is the way the lines partition the plane into (open-ended) regions, and how each region is associated with a Markoff number, as shown here:

relationship of adjacent Markoff numbers in the tree	example of adjacent Markoff numbers in the tree

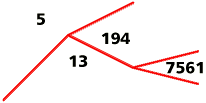
In the example shown, 7561 = 3 x 194 x 13 - 5.
Note also that 3ab-c = (a² + b²) / c
(this follows from the Markoff equation a² + b² + c² = 3abc ).
For example, 7561 = (194² + 13²) / 5.

The tree can be continued indefinitely. The numbers in regions adjacent to the 1 region in the tree as shown above (2, 5, 13, 34, 89, 233, ...) are alternate Fibonacci numbers. Numbers in regions adjacent to the 2 region (1, 5, 29, 169, 985, 5741, ...) are alternate Pell numbers.

Markoff proved that this form of tree will generate all possible Markoff numbers. A well-known conjecture states that no number appears in two places in the tree, which is tantamount to saying that no number c can be the largest number in each of two different triples (a₁,b₁,c) and (a₂,b₂,c) of positive integers that satisfy the Markoff equation. This is known as the unicity (uniqueness) conjecture for the Markoff numbers. Baragar and Button have published proofs of uniqueness for certain specific subsets of the Markoff numbers, but the general unicity conjecture remains unproven--although a faulty proof was published by Gerhard Rosenberger in 1976, and another claimed proof by Qing Zhou was withdrawn.

Markoff numbers play a role in (among other things) the theory of rational approximation of irrational numbers, but such applications are beyond the scope of these web pages. My purpose here is to describe a few interesting properties of the Markoff numbers, with an emphasis on material that doesn't require advanced math knowledge to appreciate.

More about the Markoff numbers:

• calculating Markoff numbers with matrices (updated 4 Jan 2005)
• what's with that green line in the tree?
• references
• More to come; please check back.